In the carnival ride known as the Gravitron, people stand around the perimeter of a circular chamber which begins to spin rapidly. When the chamber is going fast enough, the floor drops away, leaving people’s feet dangling. Riders feel a force pressing them against the wall, apparently holding them in place; this is known as the centrifugal force.

The cause of the centrifugal force isn’t gravity or any of the other fundamental forces of nature — it’s actually due to the rotation of the room. From an outsider’s perspective, there isn’t a force pressing the riders against the wall! Instead, the walls prevent the riders from following their natural trajectory — a straight line — so the direction of the force is actually opposite to what the riders experience, from the perspective of someone watching the Gravitron from the outside. This kind of force is known as a centripetal or “center-seeking” force.

Which observer is right: the rider, who perceives a force pushing her against the wall, or an observer outside the ride, who perceives the wall exerting a force on the rider to keep her moving in a circle? From a traditional Newtonian physics point of view (and I certainly used to teach it this way), the observer outside is right: he’s what is known as an “inertial reference frame”, one that is not experiencing acceleration. You can probably sense what is coming next, though: the traditional Newtonian physics perspective is going to fail us, not least because the smug observer who isn’t riding the Gravitron (because his wimpy little stomach can’t handle it) isn’t actually in an inertial reference frame. He’s standing on Earth, which is rotating on its axis and revolving around the Sun. He’s accelerating all the time! Admittedly, Earth’s gravity on him is strong enough that the effect of rotation isn’t huge by comparison, but it’s still there.

In any case, we’re sophisticated modern scientists here. We understand that there is no absolute frame of reference from which we can measure everything else, so nobody can smugly say “I am at rest and everything else is in motion around me, so my point of view is superior.” Everyone’s measurements are with respect to their own frame of reference; understanding how to relate measurements taken in one frame of reference to measurements taken in another frame is a major part of physics. (It’s also a common source of misunderstanding: relativity of measurement doesn’t mean everyone’s perspective is equally valid and therefore nobody is right or wrong. There’s no moral component — it’s merely a statement about measurement. Einstein himself was about as far from being a moral relativist as someone could be!) On the other hand, there is a fundamental difference between motion at constant velocity (meaning a steady speed and no change in direction) and accelerated motion. As we can see from the Gravitron example, the rider feels a centrifugal force caused by the rotation itself — that force appears simply because she is moving in a circle.

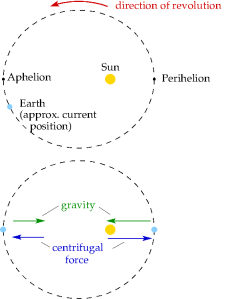
For Earth orbiting the Sun, gravity takes the place of the Gravitron wall to shape the orbital path. That adds a bit of complication, of course: Earth follows an elliptical rather than circular orbit, so the force of gravity varies over the course of a year. However, the centrifugal force Earth experiences also will vary over the course of the year: its strength depends on how fast Earth is moving. At the farthest point from the Sun where the force of gravity is weakest (the aphelion, which was a little over a month ago), Earth is moving more slowly and feels a smaller centrifugal force. At the closest point (the perihelion), both the speed and centrifugal force are larger, in the same way the gravitational force is larger.

To make things even more interesting, we can throw a third object into the mix. If the mass of the extra object is too big, the math is too complicated to resolve, but if the mass is tiny compared to Earth and the Sun, things become simple enough to let us figure out how the combined gravity and centrifugal force affect it. When you do the calculations, you find that there are five special places, known as Lagrange points (named for 18th century mathematical physicist Joseph-Louis Lagrange).

Think of the combined forces as creating a landscape, with hills and valleys. The deepest holes lie at the location of Earth and the Sun, where the gravitational forces get really big, but there will be two shallower dips (called L₄ and L₅, as shown on the figure to the right) at points equidistant from Earth and the Sun. When you draw lines connecting Earth to Sun to those Lagrange points, you get equilateral triangles — triangles whose three sides are all of equal length. It’s yet another example of the deep connection between physics and geometry. L₄ and L₅ are also known as Trojan points; the first Trojan asteroids were found at the Lagrange points in Jupiter’s orbit and named after heroes from Homer’s epic poem The Iliad.

A few weeks ago, Earth was found to have at least one Trojan asteroid, and other planets in the Solar System — including Mars and Neptune — have several identified Trojans. In addition, Saturn’s tiny moon Helene is a Trojan moon, where Saturn plays the role of the Sun and another Saturnian moon Dione is the planet-like object. (Helene is also strongly affected by Tethys and Rhea; Saturn’s moon system is very complicated!) Because the Lagrange points are empty space and the interplay of forces is complex, Trojans don’t follow circular or elliptical orbits, like planets and normal moons do; instead, their paths include shapes known as Lissajous figures (follow the link for some good simple pictures).

So much for the L₄ and L₅ Lagrange points; the other three points are like saddles in the force landscape: in one direction, the terrain falls down, while in the other it rises up. Despite the fact that these won’t be conducive to as stable orbits as a valley, objects can still orbit at those places, and in fact a number of satellites are designed to use them. The projected James Webb Space Telescope will orbit at Earth’s L₂ point; the solar observatory SOHO orbits at L₁ to provide a constant view of the Sun without ever having to pass behind Earth.

Obviously I’m simplifying the picture a lot; Rhett Allain has a great deal more at Dot Physics. However, I think it’s plain to see that although the centrifugal and other forces exhibited in rotation are not “real”, the effects are very real — and play a major part in shaping the dynamics of our Solar System. The centrifugal force is a Trojan horse to get these ideas into our minds, opening them up to a truly modern view of forces, preparing us for general relativity and a deep comprehension of the mechanics of the universe.