I originally intended this post to be “Portrait of a black hole, part 2”, but thanks to some issues I’m having with my simulation code (and the lack of time to debug them right now), I’ll hold off on that for a few more days. Instead, I thought it might be useful to elaborate on the earlier concept I introduced: the “current” analogy of spacetime. As with all metaphors, the current analogy isn’t perfect, but the more I have taught and studied and written about gravity, the more I think it’s a more valuable view than the static “rubber sheet” metaphor that we often resort to.

Let’s start with something simple: a river, flowing steadily from west to east. (I live in Virginia in the United States, so that’s a fairly typical direction for river flow.) If you are on the river’s bank, you’ll observe the flow of the water by how objects — sticks and other debris — are carried on the current. Fish and ducks and platypuses, on the other hand, might be able to swim in the opposite direction to the current, depending on the strength they exert in swimming. However, if the river’s flow is too fast, then no matter how strongly the animals swim, they will still be carried by the current, or it may require all their effort simply to stay in the same position relative to you.

Now, imagine the river is huge — bigger even than the Amazon — and you are in a rowboat in the middle of it, so far away from the banks that you can’t distinguish features on them. Without a reference to the fixed shore, you won’t detect your own motion: you’ll simply be carried along by the current insensibly. (I’m assuming there are no rocks, rapids, or sudden changes in elevation, like waterfalls.) By rowing, you can move with the flow, against it, or across it: toward or away from the banks. However, if you’re rowing toward the shore, you will still be carried by the current, so without compensating for the river’s flow, you’ll land downstream of where you’re aiming, even if you don’t notice it happening.

Whether you are the objective observer or an active participant, the river is not a passive environment: it affects the motion of objects on or under its surface to the point of sometimes dictating what kinds of motion are possible. Rapid-flowing floodwaters carry all objects with them, while lazy rivers may hardly move a floating branch. Either way, a passive object will move exactly the speed and in the direction of the flow. Animals or rowboats have a maximum speed they can move relative to the current. If their speed is slower than the river’s current, they will be borne along.

That’s the beginning of our metaphor for gravity. Spacetime is the water, the current is gravitation. Weak gravity is a lazy river, while strong gravity is raging floodwater. Objects on the river could be planets, stars, spaceships…anything affected by gravity, which includes everything. Light moves at a constant speed relative to the “current”, but otherwise behaves no differently than massive objects: its path can be affected by the flow, and if that flow is fast enough, light can even be swept away. You see, spacetime isn’t a thing: it’s the background for things. That means it can flow faster than light, though that doesn’t happen under ordinary circumstances. As we’ll see, though, the current is faster than light inside a black hole.

A single river may have fast- and slow-flowing sections, and to extend our analogy, can change direction relative to the banks. It can have whirlpools and eddies, rapids and rocks. These more complicated features are themselves metaphors: for stars, planets, galaxies, or the disturbances in spacetime known as gravitational waves. The current metaphor is even useful for understanding the expansion of spacetime that is the basis for modern cosmology, the study of the Universe as a whole. I’ll leave cosmology and gravitational waves to another day, but let’s reexamine the non-rotating black hole using the current analogy again.

Getting to the point

A non-rotating, or Schwarzschild, black hole appears the same whichever way you look at it. In mathematical terms, we say it has perfect spherical symmetry: it has no north or south pole, no equator, no axis of rotation, no bumps or irregularities. (Rotating black holes and the Sun have axial symmetry, meaning that they do have a north and south pole, but look the same under rotations around their axis. Earth is lumpy, but still has approximate axial symmetry.) That’s very convenient! Only two dimensions matter: the radial direction, which points directly toward or away from the black hole, and the azimuthal direction, which perpendicular to the radial direction. While technically there is a third dimension (the polar direction), which is also perpendicular to the radial axis, it contains no additional information we need.

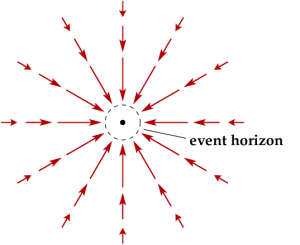
Similarly, the flow of spacetime travels directly toward the black hole. In an otherwise empty Universe, a passive object would eventually (given enough time) be pulled by the current into the black hole. Far away, the current is very weak and easily resisted. Earth is not affected by the black hole at the center of the Milky Way, much less by the larger beast at the heart of M87 galaxy. However, close in, the current grows ever stronger, flowing faster and faster until at a certain distance — the Schwarzschild radius — the flow becomes equal to the speed of light. That’s the event horizon of the black hole. Inside that horizon, closer to the black hole than the Schwarzschild radius, the current is flowing faster than light, until it technically reaches infinite speed at the mass singularity.

Matter and light aren’t passive objects, though: they have motion relative to the current. In the case of stars orbiting Sagittarius A* (pronounced “A star”), the Milky Way’s central black hole, that motion is mostly in the azimuthal direction, perpendicular to the current. As they move, the current carries them toward the black hole, curving their paths until they form more-or-less elliptical shapes.

Light passing near a black hole that doesn’t touch the event horizon will be deflected curving for a while toward the black hole before passing again on its way. In that way, a black hole can actually be visible to us by the distortion of light emitted by stars farther in the background. This effect is known as gravitational lensing. For black holes we observe, though, other effects are stronger: light emitted from orbiting matter washes it out. However, lensing is a powerful astronomical tool when the distortion is caused by galaxies or galaxy clusters.

Anything — matter and light alike — that crosses the event horizon can never escape again, because the current is flowing faster than any object can move. Once within the horizon, all paths curve toward the mass singularity at the very center, so even something with a lot of azimuthal speed won’t get out.

For objects like Earth or the Sun, which are also described by the Schwarzschild equation in general relativity, the current never reaches light-speed before whatever it carries would hit the surface. However, the basic current metaphor still works: it tells us the shape of orbits of planets, satellites, or the Moon. Now, isn’t that better than the “rubber sheet” analogy? (You should hear that last sentence spoken in a New Jersey huckster’s tones, assuming the huckster knows advanced physics.)

The flaw in the metaphor

So we beat on, boats against the current, borne back ceaselessly into the past. – F. Scott Fitzgerald, The Great Gatsby

My conscience won’t let me leave you with that, though: the metaphor isn’t perfect. First of all, spacetime isn’t a thing, so you don’t have to worry about running out of it. There can be a constant flow from infinitely far away into a black hole without bothering about where the springs for that current originate.

Also, with a real-world river, you could technically row your boat in the same direction and achieve a very fast speed. However, if you flew your spaceship at a very fast speed in the direction of the spacetime current, you still would never go faster than the speed of light, even with gravity giving you an assist. An observer watching you from a long way away (akin to the observer on the river bank watching the platypuses swimming in the original example) would see your ship approach light-speed, but because their measurements rely on light, they would see your signal grow toward ever longer wavelengths.

Once your ship is inside the horizon, an outside observer can’t see you. Since the Schwarzschild solution in its original form describes what such an observer measures, it provides no help in understanding the speed of an object once it’s inside the horizon. (Note that in my earlier post, we weren’t looking at the speed in the usual sense: we were looking at the relationship between radius and azimuthal angle, which doesn’t tell us how fast in the object is moving in the usual sense.) As we’ll see in the follow-up post on cosmology, spacetime itself can flow faster than light relative to an observer, and that can actually make objects appear to be going faster than light themselves!

As problems go, though, this isn’t a big one. As the very name of the theory tells us, physical quantities are relative: they are different depending on the frame of reference of the measurer relative to the object being measured. (There doesn’t have to be a person doing the measuring; this is “measurement” or “observation” in an abstract sense.) From the point of view of an object plunging into a black hole, the black hole is doing the moving, not the object. The force of gravity — the flow of spacetime — doesn’t exist from that frame of reference, just as you in your rowboat don’t feel the flow of the river.

As we’ll see in the next installment (assuming I can get my code working), when a black hole rotates, the current becomes a whirlpool. Any boat in that current will not just be dragged into the black hole, it will be dragged around it as it goes in a spiral pattern. That rotational dragging is part of the power of supermassive black holes at the heart of galaxies. The flow of gravity powers quasars and blazars, some of the brightest things in the Universe.